Hierarchical Triangular Mesh
The Hierarchical Triangular Mesh is a multi-level, recursive decomposition of the sphere. It starts with an octahedron and we call “level 0 trixels“ to each of its eight equilateral triangle faces. Each trixel can then be split into four smaller trixels by introducing new vertices at the midpoints of each side. Trixel division repeats recursively and indefinitely to produce smaller and smaller trixels:
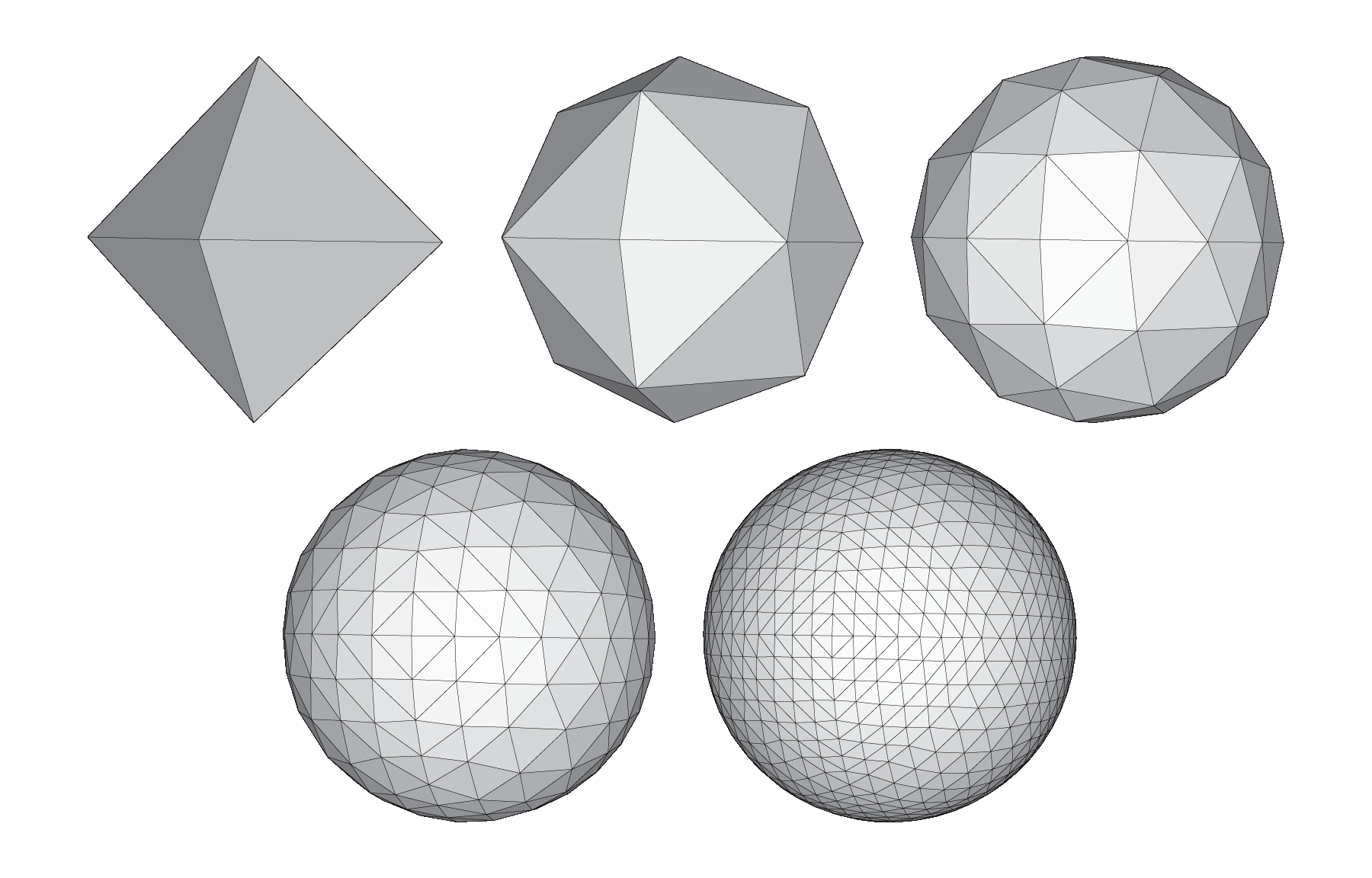
Although the division process can continue indefinitely, the internal 64-bit
representation runs out of bits at level 31 (i.e. 8 * 4^31 > 2^64).
Approximate distance (in meters) for each level is calculated using the formula:
(6371008.8 * 2 * PI / 4) / (2^level), and distance in arcseconds is calculated
using the formula: (360 * 60 * 60 / 4) / (2^level). For example, level 25 is
about 10 milli-arcseconds for astronomers or 0.3 meters on the earth’s surface:
| Level | Degrees | Distance |
|---|---|---|
| 0 | 90° | 10,007,557.22 m |
| 1 | 45° | 5,003,778.61 m |
| 3 | 11°15’ | 1,250,944.65 m |
| 5 | 2°48’45” | 312,736.16 m |
| 8 | 21’5.625” | 39,092.02 m |
| 10 | 5’16.4062” | 9,773.01 m |
| 12 | 1’19.1016” | 2,443.25 m |
| 15 | 9.8877” | 305.41 m |
| 20 | 0.3090” | 9.54 m |
| 25 | 0.0097” | 0.30 m |
| 30 | 0.0003” | 0.01 m |
An example of HTM trixels in real life can be found in the Spatial Search Tutorial.
